天大的误解:物理学是一门实验的科学
在中文物理学语境中,常听到一种说法,叫“物理学说到底是一门实验的科学”,或者“一个理论总要得到实验的验证”。这些话,如果不是完全错误,至少也是非常不恰当的,有认真举例加以讨论的必要。首先,人类能实现的实验很有限;其次,实验的直接测量结果,本质上只能是整数(别问为什么),象一维Ising模型两个最低束缚态的能量之比为这样的无理数,测量就无能为力;其次,实验数据本身不会说话,如何诠释取决于当时的物理理论甚至哲学;再其次,(稍高级复杂一点的)实验本身就是理论的,它的设计本身、执行过程和对结果的诠释都包含很多理论内容甚至假设的内容甚至连假设都没去假设的内容;最重要的是,最重要的那些物理学内容,可能是实践启发下的纯粹理性思维的结果,比如卡诺原理、惯性定律(牛顿第一定律)、广义相对论,等等。不能指望对于任何理论,都存在一个与其独立的所谓实验能够验证它的正确性。量子力学早期所依赖的光谱数据,可能和当时创立的量子力学理论是独立的,而今天的一些复杂的量子力学实验,其设计和结果诠释则很难和实验者头脑中接受的量子力学理论脱得了干系。一个单光子干涉实验,从光源到光电倍增管这一路上关于光是粒子还是波,我们的观念就来回跳跃了好几次。
以为实验在物理学中起着多么举足轻重的作用是对实验的误解,实验有时候是相当无力的,它无法指向任何结论。关于这一点,著名的例子就是引力场中两个不同质量的球是否同步下落的问题。据说,伽利略曾在意大利的比萨斜塔演示了这个实验,得出结论说两个不同质量的金属球同步下落。有史学家认为伽利略没做过这个实验。如今更有视频说宇航员在月球上演示锤子和羽毛确实是同步下落的,更显荒唐。这个实验的不可能的一个表面原因是下落过程中部分能量会转化为转动动能,另一个表面原因是针对两个不同大小的球就无法落实下落相同的高度,还有一个表面原因是根本无法做到同时让两个物体下落也无法判断它们是否同时到达某个同一高度——“同”是个很绝对的词。但是,这些都不重要。更深刻的原因是,仅凭实验数据不可能做出任何结论。排除上述问题,假设比萨斜塔为20米高,重力加速度为10 m/s2, 用精确到纳秒(ns)的现代高级计时器,所得实验结果为其一球下落时间为(2000,000,000+1)ns, 另一球下落时间为(2000,000,000-1)ns(真实的基本测量结果是整数!),误差很小吧?可是,你无法得出任何结论。一个物理学家说两球下落时间差别很小,是同步下落的,另一个物理学家说时间差别太大,下落不是同步的。怎么办? 让这两个物理学家跟如今某些大装置上的科学家一样玩锤子-剪刀-布决定结果?
这个问题的结论只能用头脑中的实验得到。若两物体不同步下落,设想质量大者在先,质量小者落后。将这两球横向加一无质量的硬连接使之成为一个物体,则此复合物体的质量更大,按照此前的逻辑,它应该比大质量的那个物体下落还快。但是,一快一慢两个物体硬连接起来的物体反而下落更快了,这样的世界有点诡异,不象是我们这个世界里的事情。反过来,假设两物体同步下落,则连接在一起的复合物体也应循相同的韵律下落,这中间不会引起任何逻辑上的矛盾。这样的结论我们比较容易接受。于是,结论是,重力场中两不同质量的物体应该同步下落。实验完毕。
以为某些物理学的结论是由实验得来的,是另一个比较流行的误解。比如,在一些文献中就有库伦用挂在马槽上的铝球壳实验得到库伦力表达式的说法。想想Charles-Augustin de Coulomb生活的年代(1736-1806.为啥不译成“德·库伦”呢),马槽上的铝球壳能得到什么精密的结果?其实,同为平方反比律的牛顿万有引力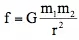 和库仑力
和库仑力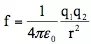 的形式,只不过是强调了我们是生活在3D空间这个事实而已。在3D空间中,一个半径为r的球其表面积为4πr2。任何一个物质流自一点向外各向同性地辐射,其流是守恒的,则其流密度总是和4πr2成反比。剩下的就是在源和作用之间找个合适的比例因子而已,那个4π的处理很有趣:牛顿定律中没顾及4π的问题,结果4π就得和万有引力常数相乘后才是合适的比例因子,这个不方便一直被带到爱因斯坦的广义相对论方程。得到平方反比律公式是理性思考的结果,不是根据哪个实验数据能建立的。牛顿拿平面几何学知识证明了平方反比律的力场中行星绕太阳的轨道确实(可以)是一个椭圆时,这个law就被接受了而不再需要乞灵于任何人的测量数据。倘若依据精密的实验数据,得到的库仑力形式是
的形式,只不过是强调了我们是生活在3D空间这个事实而已。在3D空间中,一个半径为r的球其表面积为4πr2。任何一个物质流自一点向外各向同性地辐射,其流是守恒的,则其流密度总是和4πr2成反比。剩下的就是在源和作用之间找个合适的比例因子而已,那个4π的处理很有趣:牛顿定律中没顾及4π的问题,结果4π就得和万有引力常数相乘后才是合适的比例因子,这个不方便一直被带到爱因斯坦的广义相对论方程。得到平方反比律公式是理性思考的结果,不是根据哪个实验数据能建立的。牛顿拿平面几何学知识证明了平方反比律的力场中行星绕太阳的轨道确实(可以)是一个椭圆时,这个law就被接受了而不再需要乞灵于任何人的测量数据。倘若依据精密的实验数据,得到的库仑力形式是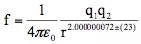 ,这样的物理学你愿意学?况且,物理的世界里就不需要力这个概念。扯远了!
,这样的物理学你愿意学?况且,物理的世界里就不需要力这个概念。扯远了!
另一个纯由理性思考得来的重要定律是牛顿第一定律,即惯性定律。这个定律的得来依赖于实验观察(的启发),但不可能由实验得到。让一个小球从一个斜面滚下,对面由一个不同倾角的斜坡接着,小球爬上对面斜坡一定高度后又会滚下来。实验发现,如果摩擦力足够小,不管对面斜坡的倾角多大,从一定斜坡滚下的小球,在另一个斜坡上大致会爬上一个相同的高度。实验能做的到此为止,接下来纯粹理性思维该登场了。既然爬上大致相同的高度与斜坡的倾角无关,则倾角越小,小球爬上这样的高度需走过的路径就越长。如果倾角趋于零,则小球需要走过无穷远的路,也即是说,从一个斜坡滚下到平面上的小球,因为不再受别的力(其实是受力平衡),它会一直向前运动。换成更学术一点的说法,就是“一个物体将保持其运动状态不变,除非受到了来自其它物体的作用”, 这就是惯性定律。它来自实验,又不是完全来自实验。实验和理论从来就不是割裂的。
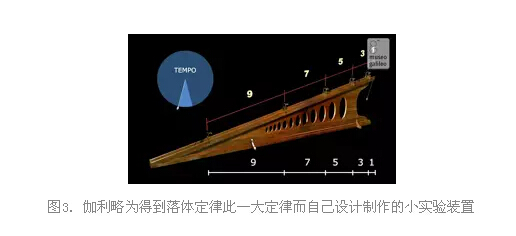
实验是一门需要天才的艺术。如何做实验的一个伟大典型范例,我可以举伽利略是如何得到落体定律h=at2的为例。想象一下伽利略那时一没有计时器(挂钟还在等他的原理性发明呢),二是在他能获得的条件下落体时间不过两秒左右,他都没法得到不同时刻落体的位置。伽利略该怎么办?向政府申请大笔经费?关键是钱不能解决思想贫乏的问题啊。伽利略首先想到用斜坡也能得到下落过程的规律——自由下落就是在90°斜坡上的滚动(我做了30年实验都没曾有过一个这样天才的想法)。斜坡可以延长下落时间,使得记录位置成为可能。他把斜坡的坡度降到了17°。其次,他在斜坡上安放一些位置可调的小铃铛,小球滚过碰响铃铛,而这铃铛响的间隔可以用来标志时间(图3)。伽利略用自己的脉搏和哼唱的曲调来计时(粗略地计时。没思想的精确数据有啥用!),调整铃铛位置,使得他用脉搏和哼唱标记的小球滚过两个铃铛之间距离的用时大概是相等的。这样,相邻铃铛之间的距离是小球在下落不同时期在同样长度的时间间隔内滚过的。测量铃铛之间的距离,发现它们之间的间距之比近似地(很粗糙的近似。没思想的精确数据有啥用!!)为1:3:5:7:9……, 也就是说在n个时间单位内,小球下落过程中滚过的距离为n2个距离单位,因此落体定律应为h=at2,其中a是未知的比例系数。怎么样,这才叫实验。
不能指望用实验去解决我们的所有物理问题甚至去由此制造物理问题。在物理学中,许多物理参数对应的空间是人类无法达到的,是no man’s land。温度和压力是两个典型的热力学中的强度量,作为强度量它们都有一个共同的特性,就是绝对零值不能达到(这是康德先阐述的),因此追求温度和压力的无限趋于零是一个无止境的过程。如果某位物理学家因为一个崇高的科学目标一直追求绝对温度趋于零,这一个研究项目就足以让全人类破产。另一个伟大的物理目标是到更小的空间尺度上去研究物理,这需要不断增高的粒子能量,相应地,粒子加速器的块头和消耗也会指数攀升。据说,为了验证超弦理论这个猜想之上的伟大猜想所需的加速器,其长度应该环地球一周甚至更长。做这样的实验,愚公精神是必须的。
关于物理的理论与实验,有个有趣的傻瓜定理,学物理的人不妨知道。做理论的,提出一个理论模型,除了他自己当真谁都不当真;做实验的,给出一组实验数据,谁都当真就他自己不当真。拿实验数据当真,说明对物理实验不了解,可能却又同时伴随着对物理实验的轻视。我一个做理论物理的朋友曾当着我的面说,研究生面试不合格的同学也应该留下,做不了理论物理可以去做实验嘛。这反映的是我们这里比较普遍的关于实验的错误认知。好的实验从来都是理论的,从构思实验,到设计、建造实验设施再到实验数据的处理与诠释,都需要深厚的数学、理论物理和metaphysics(形而上学)的功底。我最得意的文章是拿汪卫华院士课题组的金属玻璃断裂照片配第一位诺贝尔文学奖得主Sully Prudhomme的法文诗le vase brisé(带裂痕的花瓶)一起发表的。我们的学生只知道费曼物理学讲义和朗道理论物理教程这样比较技术性的教科书系列,对泡利物理学讲义这样有些思辨的就不太感冒,而对于Bergmann-Schäfer实验物理教程这样比较细碎的教科书系列则是闻所未闻。许多做实验的朋友,可能从未读过数学家、理论物理学家Clifford关于长度、质量等基本量测量之common sense的讨论,未读过哲学家康德关于各种物理量表现的讨论,未读过恩格斯的《自然辩证法》与《反杜林论》中一些关于物理定律如何得来的讨论,甚至有人不知道温度计从来测的不是温度。不是把买来的仪器接上电,悠闲地看着计算机终端输出精美的曲线或者图像就叫做实验的。不知道实验背后的理论物理与数学,不知道实验结果得以诠释的哲学思辨,就敢拿国家大把的钱动员几百上千人去做大实验,这种可嘉的勇气也令人肃然起敬,但对这样实验的结果怕是不能抱什么希望。物理学的许多实验是靠设备的,这是不争的事实,但不往实验设备和实验过程中灌注思想,肯定不是正确的物理实验模式。
真正的物理实验是思想的极致,真正能得出物理结论的实验室就在物理学家的肩膀上。等到更多的人学会了用头脑去做实验,中国的实验物理事业就有希望了——我们一起期待着。

